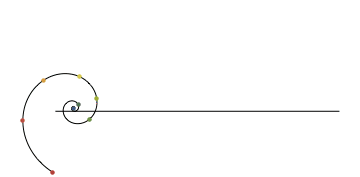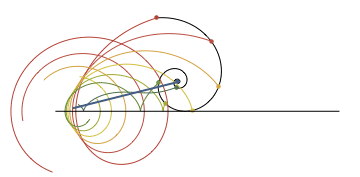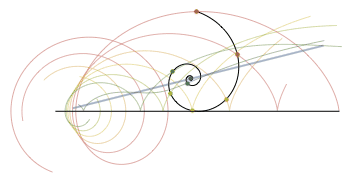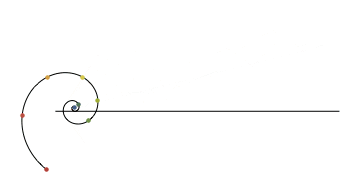Espiral logarítmica: Llegamos por fin a la que seguramente sea la más fascinante de las espirales. También conocida como Espiral de Bernouilli y Espiral de Fibonacci, esta curva está estrechamente relacionada con el número de oro.
La gran diferencia de esta espiral con la de Arquímedes, es que el radio de curvatura respecto del centro crece cumpliendo una progresión geométrica. Esto quiere decir que en vez de crecer ese radio de forma constante, crece respecto al producto de valores anteriores. Es por eso que crece, y por tanto se aleja del centro, mucho más rápido que otras espirales.
Es fascinante ver cómo aparece esta curva en la naturaleza habitualmente. Desde conchas de moluscos, hasta la formación de galaxias, pasando por la forma que toman los huracanes o los girasoles.
La magia de los girasoles habita en todo su ser: desde sus semillas y su aceite llenos de nutrientes, la forma en que sus pétalos siguen el sol, hasta el secreto matemático que encierran sus espirales.
El patrón de las semillas dentro de la cabeza de un girasol sigue la secuencia Fibonacci: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etcétera. Cada número de la secuencia es la suma de los dos anteriores (55=34+21).
En los girasoles, las espirales de su centro crecen en esta proporción. (Cuenta el número de curvas que crecen en una dirección, del centro a los pétalos, y luego las que crecen en sentido opuesto).
Esto sucede en muchas otras plantas y flores. Crecen en espirales, desde el centro hacia afuera. Esto es para que las nuevas hojas no bloqueen el sol de las anteriores, o para cubrir el máximo de superficie para recibir lo más posible de lluvia.
También es por esto que si cuentas el número de pétalos de una flor, margarita o girasol, verás que corresponde a algún número de la serie de Fibonacci (en promedio, algunos pétalos se pudieron caer al crecer).
Espiral de Fermat
Espiral de Fermat: También conocida como espiral parabólica, es una espiral bastante especial y difícil de encontrar de forma natural. Se puede
decir que es un caso especial de la Espiral de Arquímedes, pero su fórmula (que es bastante complicadilla de entender si no sabemos coordenadas polares) tiene una raíz cuadrada, por lo que cada caso tiene dos soluciones. Es decir, a cada valor del ángulo le corresponden dos valores del radio, uno de ellos positivo y el otro negativo.
decir que es un caso especial de la Espiral de Arquímedes, pero su fórmula (que es bastante complicadilla de entender si no sabemos coordenadas polares) tiene una raíz cuadrada, por lo que cada caso tiene dos soluciones. Es decir, a cada valor del ángulo le corresponden dos valores del radio, uno de ellos positivo y el otro negativo.
Para aclararnos, es como si fueran dos Espirales de Arquímedes, que salen desde el mismo centro (por tanto ese punto es común) y después cada una va hacia un lado distinto.
Espiral hiperbólica
Espiral hiperbólica: Es justamente el caso inverso a la Espiral de Arquímedes. Empieza desde un radio muy grande (infinito) y ese radio va disminuyendo hasta llegar al centro de la espiral.
De esta espiral cabe destacar que es fácil de encontrar en la naturaleza, ya que muchos moluscos tienden a crecer cumpliendo su forma.
Espiral logarítmica
Espiral logarítmica: Llegamos por fin a la que seguramente sea la más fascinante de las espirales. También conocida como Espiral de Bernouilli y Espira
ESPIRALES Y SUS APLICACIONES
Clotoide
Espiral de Cornu o clotoide ocoloide o clotoide (x,y)=(C(t), S(t)). La espiral converge al centro de los dos remolinos extremos de la imagen, a medida que t tiende a más infinito y menos infinito.
La curva que une la recta y la circunferencia es la clotoide. Se caracteriza por variar su curvatura desde la recta (curvatura = 0) hasta la de la circunferencia con curvatura dada.La clotoide, también denominada radioide de arcos o espiral de Cornú en honor de Marie Alfred Cornu, es una curva tangente al eje de las abscisas en el origen y cuyo radio de curvatura disminuye de manera inversamente proporcional a la distancia recorrida sobre ella. Es por ello que en el punto origen de la curva, el radio es infinito.
en esta parametrización el vector tangente tiene longitud unidad y t es la longitud de arco medida a partir de (0,0) (e incluyendo signo), de lo que se deduce que la curva tiene longitud infinita.
Aplicaciones
La espiral de Cornu tiene la propiedad de que su curvatura en cualquier punto es proporcional a la distancia a lo largo de la curva medida desde el origen. Esta propiedad hace que sea útil como curva de transición en el trazado de autopistas o ferrocarriles, puesto que un vehículo que siga dicha curva a velocidad constante tendrá una aceleración angular constante. Así dicha curva se utiliza para acuerdos planimétricos en trazados de carreteras y, especialmente, ferroviarios (salvo aprovechamiento de explanada anterior para el que se utilizan otras curvas de acuerdo), con el fin de evitar discontinuidades en la aceleración centrípeta de los vehículos. La curva de transición que resulta tiene radio infinito en el punto tangente a la parte recta del trazado, y radio R en el punto de tangencia con la curva circular uniforme, de esta manera el tipo de curva en carreteras es tramo recto-clotoide-circular-clotoide-tramo recto salvo para curvas circulares de radio mayor que cinco mil metros (< 5 000 m) en carreteras de los Grupos 1 y 2 y para curvas circulares de radio mayor que dos mil quinientos metros (< 2 500 m) en carreteras del Grupo 3.
Igualmente las secciones de esta espiral clotoide son usadas comúnmente en montañas rusas por lo que algunas vueltas completas se conocen como loops "clotoides".
En el diseño geométrico de vías, normalmente usado en el trazado horizontal.
Historia
En los primeros ferrocarriles, debido a las bajas velocidades y los grandes radios utilizados en curvas hicieron posible que se ignorara cualquier tipo de transición entre curva y recta. Es a partir del siglo XIX cuando los incrementos de velocidad dan la necesidad de curvas que cambien gradualmente su curvatura. En 1862 Rankine en su obra "Civil Engineering" ya cita algunas curvas que podrían utilizarse, entre ellas una propuesta de 1828 o 1829 llamada "curva de los senos" de William Gravatt y la curva de ajuste de William Froude de 1842 que aproximaba una curva elástica. La actual ecuación dada por Rankine es la de una curva cúbica, o polinómica de grado 3.
EL PROBLEMA ECONÓMICO DE LAS RELACIONES ´
ÍNTER INDUSTRIALES
El análisis de cuadros de insumo-producto, fue desarrollado por W.W. Leontief en 1936, como el instrumento de interpretación de las interdependencias de los diversos sectores de la economía. Es decir, en el análisis de insumo-producto consideramos cualquier sistema económico como un complejo de industrias mutuamente insurreccionadas. Se considera que toda industria recibe materias primas (insumos) de las demás industrias del sistema y que, a su vez, proporciona su producción a las demás industrias en calidad de materia prima. Fundamentalmente se trata de un análisis general del equilibrio estático de las condiciones tecnológicas de la producción total de una economía, durante el periodo de tiempo en cuestión.